










お取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った低価格のスペクトル密度計算サービスを開始致しました。詳細は->ここ<-をクリックください。
このページは当事業所で提供するデータ解析業務について、これらの計算の内容の簡単な紹介及びこれらの計算がどのような役に立つのかということを説明するページで、数式や学術用語の使用はできるだけ避けています。このため一部の表現は数学的には厳密ではありません。
このページで紹介している以外の項目については、上の”データ解析”のボタンをクリックして下さい。データ解析のページに記載していないような項目でも計算可能な場合がありますので、データ解析のページに記載していないような項目の計算を希望される場合はメールでお問い合せ頂きますようお願い致します。
パワースペクトル密度関数とは(power spectral density function)
パワースペクトル密度関数は時系列データについて、どの周波数(又は周期)で変動が大きいかを示します。単位は分散/周波数(幅)で、この値を適当な周波数域で積分すると、その時系列データのその周波数域での変動のエネルギーを表す分散(分散とエネルギーの関係については->ここ<-をクリックください)が計算できます。
パワースペクトル密度関数の有用性
パワースペクトル密度関数は、時系列データ中に周期的な変動がある場合、その成分を検出する際に便利な道具となります。例えば工場などでモータなどによる振動が製品の品質に悪影響を与えている場合、音その他を記録してそのデータのパワースペクトル密度関数の分布を調べると振動の周波数がわかりますので、どのモータが原因であるかの推定に役立てたり、防振対策に利用したりできるかもしれません。また、パワースペクトル密度関数より、周期的な変動の大きさがわかりますので、例えばアイスクリームの販売数の数年分のデータより、数年以上の時間による長期的な傾向より季節的なアイスクリーム販売数の変動を分離して見積もることができたりします。
当事業所では時系列データ解析を行う場合、データの性格を把握するために平均や標準偏差といった一般的な統計計算と同じように初期段階でパワースペクトル密度関数の計算を行います。普通の時系列プロットを作成し、それを眺めることももちろんデータの一般的な性格を把握するためには大変有用ですが、パワースペクトル密度関数を用いるとデータの変動がどういった周波数で大きいのかといったことが容易に把握できますので、この情報を基にそれ以後の解析でどの周波数域を重点的に調べるかといった方針を立てる事に利用できたりしますので大変便利です。
パワースペクトル密度関数の例
ここでは例として太平洋赤道で観測された流速の東西成分の変動のパワースペクトル密度関数を示します。あまり一般の方が関心を持たれるようなデータではないと思いますが、時系列データということでは特別に変わったデータでもないということで、ご容赦ください。
さて、図1aがパワースペクトル密度関数の分布です。横軸は単位が日の周期で、縦軸が分散/周波数(幅)となります。海洋の場合は、潮汐のように周波数が一定の変動はその周波数でのみピークとなるようないわゆる線スペクトルとなります。図1aの場合、潮汐成分は周期が約1日の日周潮(*D)、約半日の半日周潮(*SD)がはっきりとしたピークで示されています。その他緑の*で示されたものも多分潮汐成分と思われますが、どこでも観測されるような周期のものではありません。
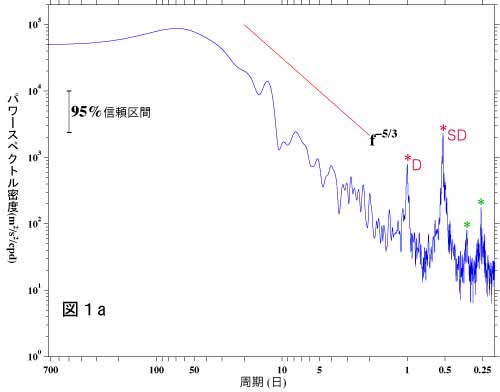
こういった周波数が一定の潮汐のような変動を除くと海洋のデータのスペクトル密度の分布にはある程度の幅の周波数域にわたって値の大きな部分があり、それより高い周波数(短い周期)域では周波数が増加(周期が減少)するにつれエネルギーが指数関数的に減少するような部分が見られるのが一般的です。こういった部分では値のおおきな部分で大気の変動などによりエネルギーが海洋に与えられ、この与えられたエネルギーが非線形作用と呼ばれる作用によって海洋内部で高周波数域に伝えられています。もっと高い周波数部分では粘性の作用により、運動エネルギーが熱に変換されて逸散されてしまいます。
図1bにこのデータの時系列プロットを、図1cにこのデータの最初の240個のみの時系列プロットを示します。このデータのサンプリング間隔は1時間ですので、図1cは10日分のデータになり、この中に1日周潮の潮汐は10回、半日周潮の潮汐は20回変動している筈なのですが、この図ではあまりよくわかりません。適当な数値フィルタを適用すれば潮汐成分の変動はかなり見やすくなりますが、パワースペクトル密度関数を計算すると、そのような手間をかけずに潮汐成分の存在がその周期や振幅といった情報や潮汐以外の周期の変動のもの迄含めて容易に把握することができます。
パワースペクトル密度関数の問題点
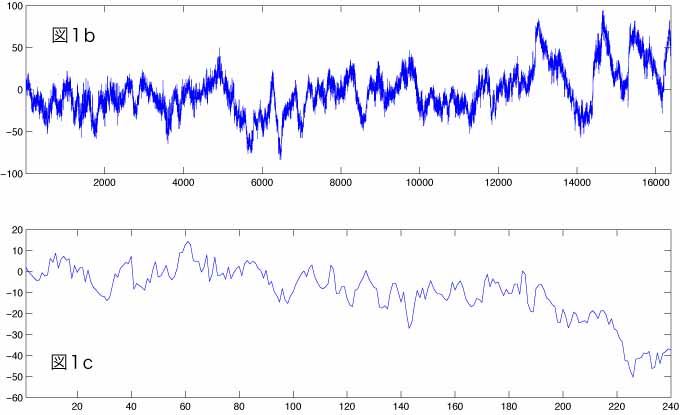
パワースペクトル密度関数の問題点というと、やや大げさなのですが、パワースペクトル密度関数を利用する場合に注意しなければならない場合があります。図2の左の列にここで例として用いた5組の時系列データの時系列プロットを、図2の右の列にこれらのデータから計算したパワースペクトル密度を示します。左の列の各図の水平の黒の破線はゼロレベルを示しています。また、右の列の各図の縦軸はパワースペクトル密度です。
まず、1段目の最初にパルスがひとつ入っているデータですが、この場合のパワースペクトル密度は、周波数によらず一定となります。この例の場合、パルス以外は何もないデータなのですが、普通のデータに何らかの理由で比較的強いパルス状のノイズが1回入ったりすると、そのノイズのため、パワースペクトル密度が全周波数域で一様に大きくなり、ノイズ以外の部分が分かりにくくなる可能性があります。
次に2段目の周期的なパルスがある場合ですが、この場合パワースペクトル密度はこのパルスの発生周波数にピークが現れますが、それ以外にも一定の間隔でピークが現れます。例えばモータのようなものが一定周期でスパークを発生して、それがデータに混入するといった場合、このような状況が発生するかもしれません。
次に、3段目でデータの波形が矩形(四角)の場合ですが、この場合も矩形波の周期以外に一定の間隔でピークが現れます。論理回路では矩形波は珍しくないですが、実際にはこのような一定の幅の矩形波はクロックの出力以外は多分あまりないので、この例はあまり良い例ではないかもしれません。一般的なデジタルデータの伝送に必要な帯域幅を見積もるといった用途ではパワースペクトル密度が使われることもあるようです。
ここ迄記述した”問題点”は、パワースペクトル密度関数は時系列データを周波数の異なる正弦波(4段目が正弦波です)が足し合わされたものとして捉えることによります。矩形波の立ち上がり部分から平になる辺りの波形は急な角になっていますが、こういった部分を再現するためには非常に多くの周波数の正弦波を足し合わせる必要があります。このような理由で、パワースペクトル密度関数にはデータに含まれる信号の周波数(パルスの場合パルスの発生周波数。矩形波の場合矩形波としての発生周波数)以外にもピークが現れる事になります。
では、4段目のように入力データがきれいな正弦波の場合ではどうでしょうか?この場合はパワースペクトル密度関数は唯一つのピークを示すだけです。なお、右列の図ではピークは幅をもっていますが、これはパワースペクトル密度を計算する場合、その推定の精度を上げるためにスペクトルウィンドウをかけるといった操作(詳細は->ここ(FDSと表記)<-をクリックください)を行った結果によります。パワースペクトル密度関数の計算の場合、振幅の精度を上げるためには、周波数の精度を下げる必要があり、結果としてピークの幅が広くなります。
最後の例として、5段目で正弦波のピークを切ってみました。図では見づらいとは思いますが、4段目の正弦波は振幅は1.0としていますが、5段目ではこのデータの値が0.95以上は0.95に、-0.95以下は-0.95にすることにより、正弦波の頂きを平にしています。この場合はパワースペクトル密度関数に複数のピークがでてきます。正弦波をアンプに入力したところ、飽和してしまったような状況でしょうか。時系列プロットでは一見よくわからないようなことも、パワースペクトル密度関数を見ればすぐわかるという例になるかと思います。
最後に1つお断りしなければならない事があります。図2で示した結果は言わば最善の結果で、実際の計算ではスペクトル漏れ(詳細は->ここ<-をクリックください)と呼ばれる現象で入力データがまったく同じでもデータの長さ次第ではピークの巾が図2に比べ相当広がる場合があります。
なお、パワースペクトル密度関数の詳細については当事業所が提供する小額定型計算業務PD001A/Bのユーザガイドの第2章、第4章及び補足に記述していますので、必要があればそちらをご参照ください。
相互スペクトル密度関数
2組の時系列データがある場合、その両方より、相互スペクトル密度関数が計算できます。相互スペクトル密度関数は、それ単独で用いられるよりは、スペクトル密度関数と組合せ、コヒーレンスやその他の関数を計算して用いられる方が多いようです。また、2組以上の時系列データの総合的な関連を調べたい場合は、相互スペクトル密度関数は周波数領域の主成分解析(EOF解析)にも利用できます。なお、相互スペクトル密度関数は相互相関関数のフーリエ変換となります。
お取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った低価格のスペクトル密度計算サービスを開始致しました。詳細は->ここ<-をクリックください。
お問合せは
->こちらへ<-